4.4. Arte cinético y arte óptico
4.4.4. Ejemplo: creemos movimiento sobre una obra de Georg Nees
Ya trabajamos a George Nees (1926-2016) en el reto 2. Fue uno de los primeros investigadores, teóricos y artistas del arte digital. Se le considera un pionero y fue el primero en exponer dibujos generados por ordenador en la Universidad de Stuttgart en febrero de 1965, con piezas de Friedrich Nake y Michael Noll (consultad el apartado sobre arte computacional: 4.1.3. «Primeros gráficos por computadora: de la experimentación a la exhibición»).
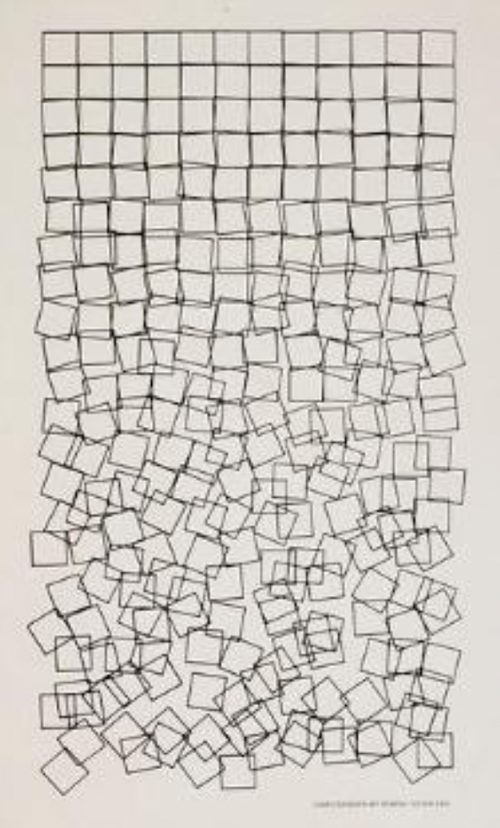
En este ejemplo trabajaremos a partir de su obra Schotter y le daremos vida con Snap! Para hacerlo, nos inspiraremos en el trabajo de Selim Tezel, que después de escuchar una conferencia de Joachim Wedekind decidió crear una revisión de la obra de Nees pero con movimiento, como si fuera una cascada de cuadrados continua. Tezel utilizó Scratch como lenguaje de programación, pero nosotros lo haremos con Snap!
El ejemplo nos servirá para explicar qué es un clon y cómo los podemos usar cuando programamos con Snap! Aquí tenéis el código del programa entero que analizaremos a continuación. Y este es el efecto final que queremos conseguir:

Como veis, en la obra de Nees tenemos numerosos cuadrados. En nuestro programa solo tendremos uno, del cual iremos extrayendo clones. Los personajes de Snap! pueden crear un clon de sí mismos en cualquier momento del programa, y podemos definir exactamente qué harán estos clones cuando sean creados. Hay dos instrucciones básicas para hacerlo: «crea un clon de mí mismo» y «cuando una copia de mí empiece».

Centrándonos en nuestro ejemplo, necesitamos un personaje que sea un cuadrado (podemos dibujarlo con el Paint de la Snap! o abrir una imagen de un cuadrado). Para empezar, crearemos un nuevo bloque llamado «MakeRow», que nos servirá para crear una fila de diez clones. Lo haremos así:
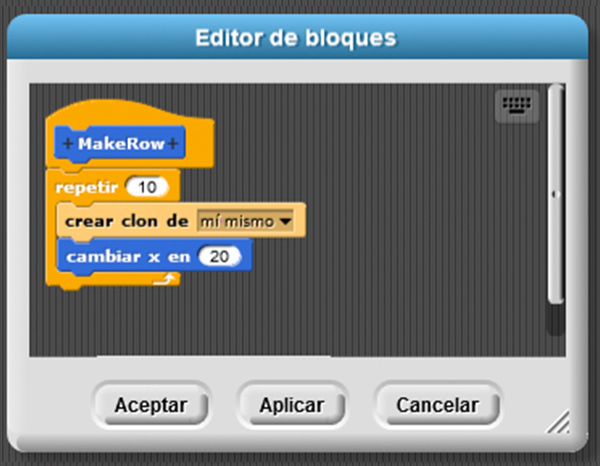
Una vez hecho esto, podemos construir el programa principal, que consiste en un bucle «para siempre» en el que vamos creando filas de clones y volvemos a la posición inicial.
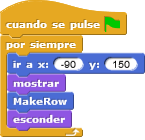
Y ahora queda programar la parte más importante, que es la que dice a cada clon cómo debe comportarse.
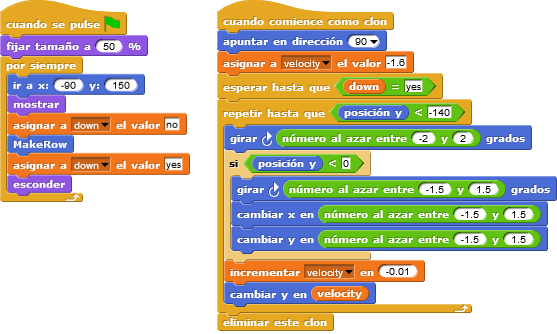
Fijaos en el comportamiento de cada cuadrado en la animación de arriba. Sencillamente se van moviendo hacia abajo hasta que desaparecen a partir de una cierta altura. Y, mientras bajan, primero solo van girando aleatoriamente unos cuantos grados, pero a partir de una altura determinada también empiezan a hacer pequeños desplazamientos aleatorios además de los giros. Lo podemos hacer con este programa:
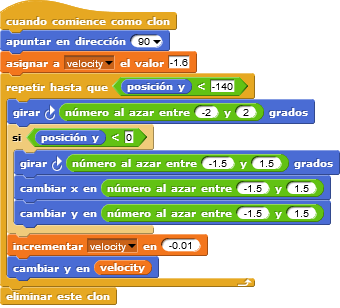
Así pues, cada cuadrado repite todas estas instrucciones cuando nace hasta que llega a una posición Y por debajo de –140. Entonces se autoelimina mediante la instrucción «borra este clon».
En «repite», en cada iteración sumamos un valor negativo a la Y para que el cuadrado vaya bajando. Este valor que sumamos a Y lo tenemos guardado en la variable «velocity», la cual vamos incrementando con cada iteración, para que así vaya bajando cada vez más rápido. El resto de bloques son pequeños giros y desplazamientos aleatorios, que se acentúan cuando el cuadrado llega a una posición Y por debajo de 0.
Si ejecutamos el programa con el código que hemos visto hasta ahora, la salida por pantalla sería como la siguiente. Las filas están inclinadas, y este es un efecto que deberíamos corregir. El motivo para que esto pase es que cuando un cuadrado nace no se espera que se haya completado toda la fila para empezar a bajar. Y, por lo tanto, cuanto más a la izquierda más abajo están los cuadrados, porque ha pasado más tiempo desde que han sido creados y han tenido más tiempo para bajar.

Podemos corregir este problema añadiendo una variable «down», que inicializamos con un «no» justo antes de crear la fila y actualizamos con un «yes» nada más acabar la fila. Ahora solo tendremos que añadir una instrucción «espera hasta down = yes», justo antes del «repite» que controla el comportamiento de cada clon. Así, nos aseguramos de que los cuadrados no se empiezan a mover hasta que hemos acabado de construir la fila entera.